git生成diff原理：Myers差分算法

什么是Myers差分算法

举一个最常见的例子，我们使用git进行提交时，通常会使用git diff --cached来查看这次提交做了哪些改动，这里我们先简单定义一下什么是diff：diff就是目标文本和源文本之间的区别，也就是将源文本变成目标文本所需要的操作。Myers算法由Eugene W.Myers在1986年发表的一篇论文中提出，是一个能在大部分情况产生”最短的直观的“diff的一个算法。

diff与图搜索

”寻找最短的直观的diff”是一个非常模糊的问题，首先，我们需要把这个问题抽象为一个具体的数学问题，然后再来寻找算法解决。抽象的过程交给算法科学家了，抽象的结果是：寻找diff的过程可以被表示为图搜索

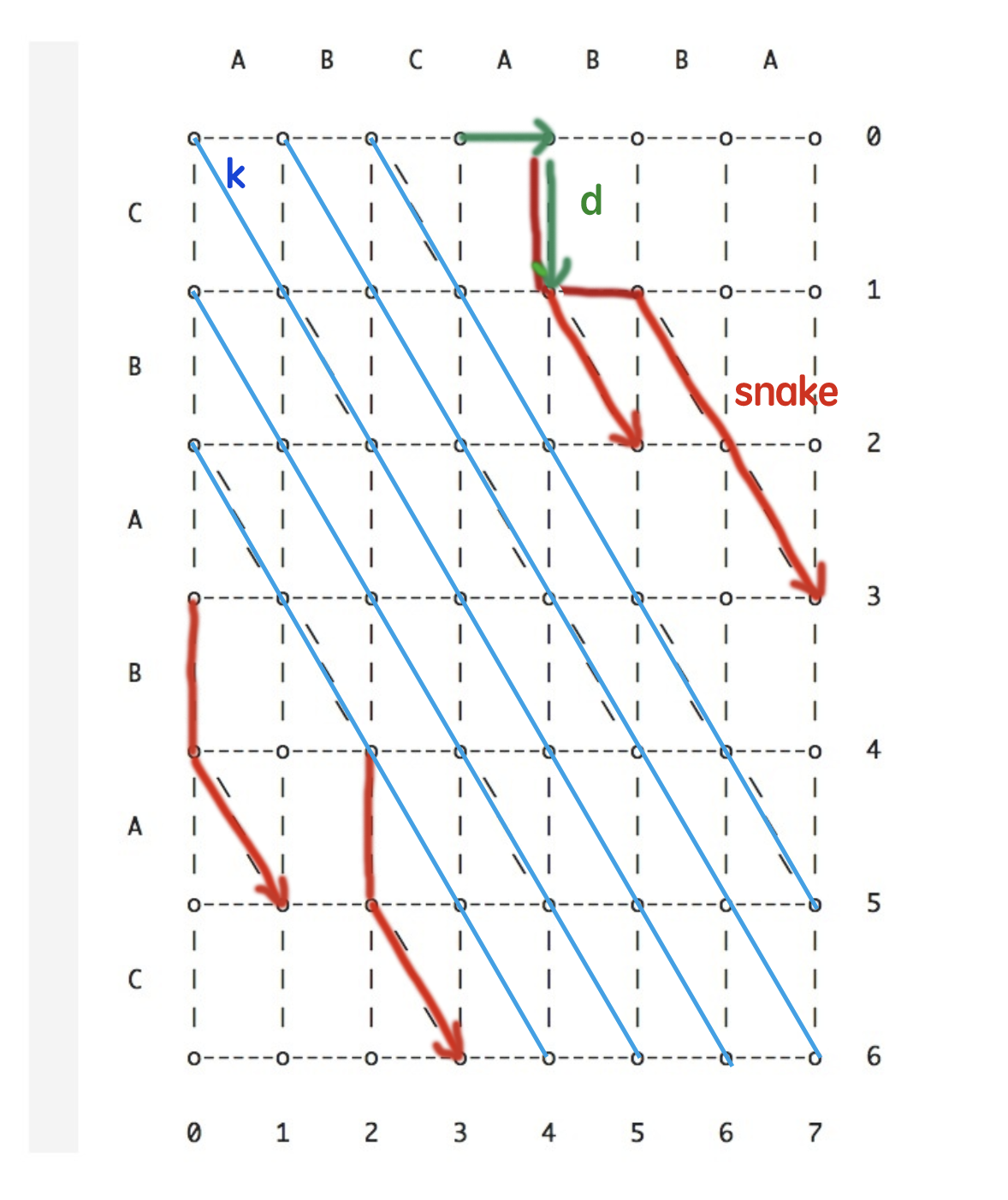
什么意思呢？还是以两个字符串，src=ABCABBA，dst=CBABAC为例，根据这两个字符串我们可以构造下面一张图，横轴是src内容，纵轴是dst内容，那么图中每一条从左上角到右下角的路径，都表示一个diff。向右表示删除，向下表示新增，对角线则表示原内容保持不动

根据图中形成的线路，我们可以选择一条路径看看它的效果

现在，“寻找diff”这件事，被抽象成了“寻找图的路径”了。那么，“最短的直观的”diff对应的路径有什么特点呢？

• 路径长度最短（对角线不算长度）

• 先向右，再向下（先删除，后新增）

三个概念

根据 Myers 的论文，他提出了三个概念：

• snake: 一条snake代表走一步。例如从(0,0)->(0,1) / (0,0)->(1,0) / (0,1)->(0,2)->(2,4) 这分别为三条snake，走对角线不计入步数。

• k line: 定义 k = x - y （我们可以写成 y = x - k，是相同斜率的平行斜线组成的一个集合)

• d contour: 走一步算一个d

算法原理

根据路径图与提出的三个概念，我们可以画出如下一张图，横坐标代表d（步数），纵坐标代表k（偏移），图中每一点代表最优坐标

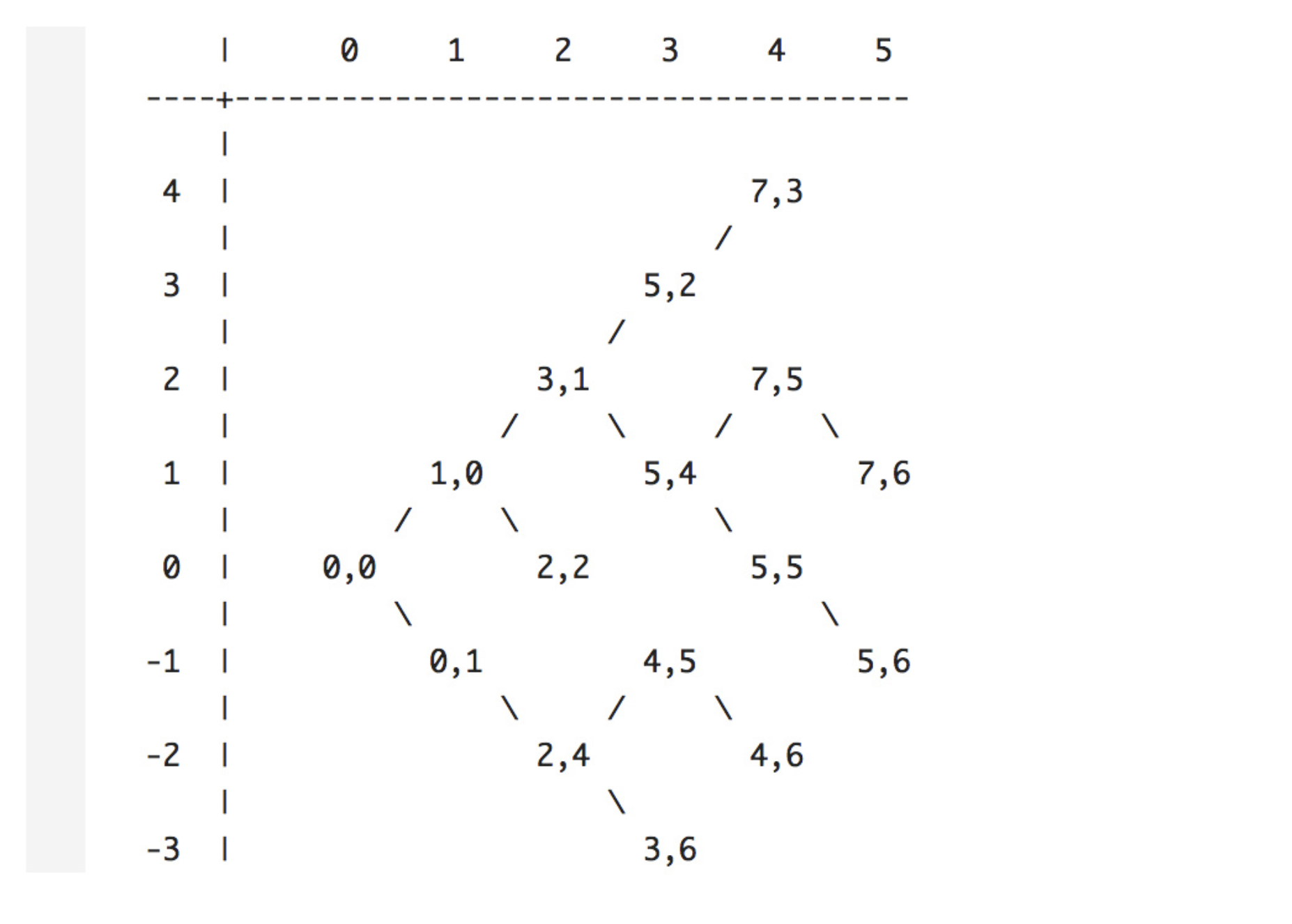
现在我们可以知道，其实Myers算法是一个典型的动态规划算法，也就是说，父问题的求解归结为子问题的求解。要知道d=5时所有k对应的最优坐标，必须先要知道d=4时所有k对应的最优坐标，要知道d=4时的答案，必须先求解d=3，以此类推

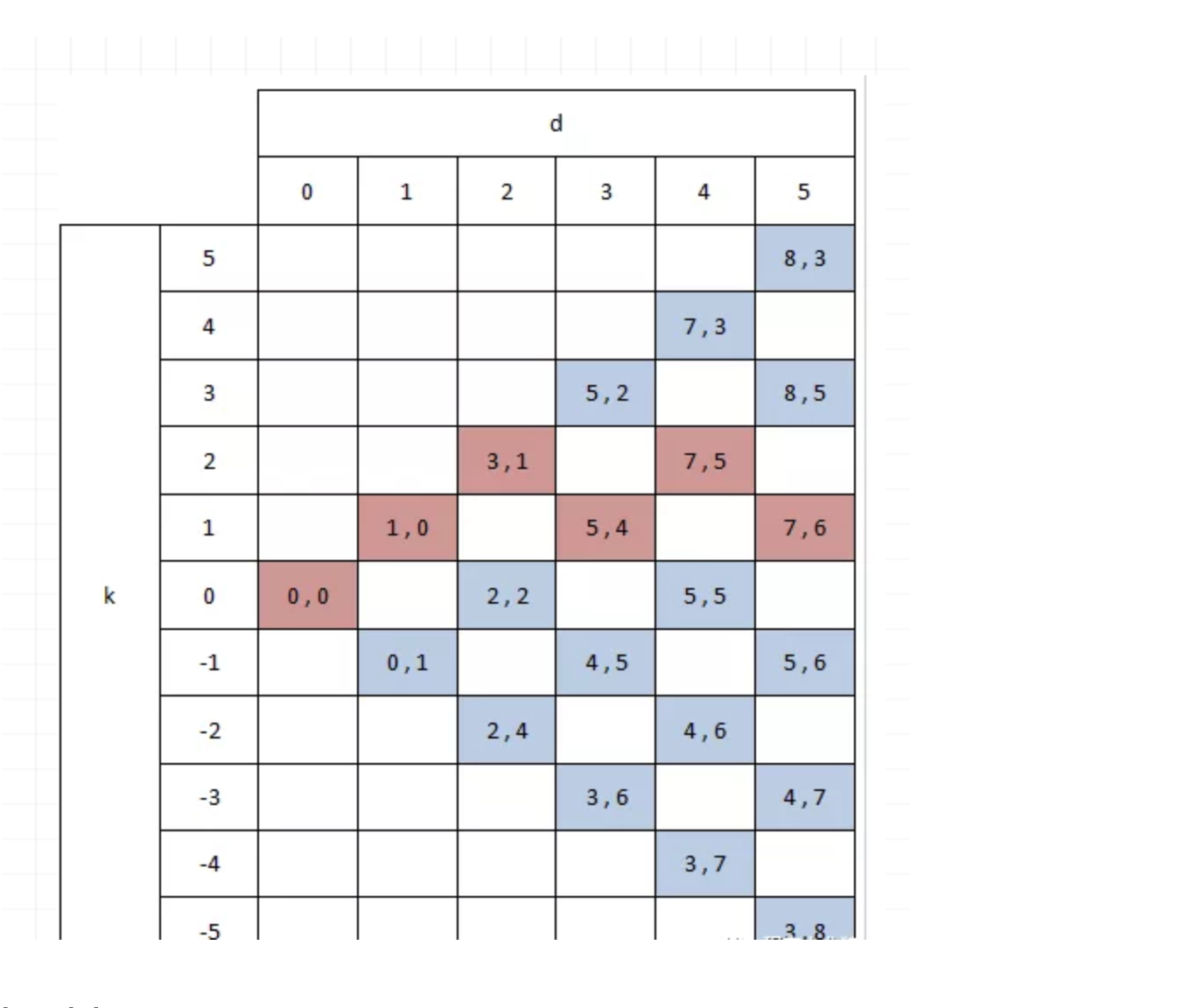
根据上图，我们也能直观的看到到达（7，6）的最短路径，见下图

算法实现（java）

外层循环步数d，内层循环偏移k，两个for循环找出最短diff路径

• 定义抽象基础节点PathNode，及实现类DiffNode（做操作的节点），Snake（对角线节点）

public abstract class PathNode {
    public final int i;
    public final int j;
    public final PathNode prev;

    public PathNode(int i, int j, PathNode prev) {
        this.i = i;
        this.j = j;
        this.prev = prev;
    }

    public abstract Boolean isSnake();

    @Override
    public String toString() {
        StringBuffer buf = new StringBuffer("[");
        PathNode node = this;
        while (node != null) {
            buf.append("(");
            buf.append(Integer.toString(node.i));
            buf.append(",");
            buf.append(Integer.toString(node.j));
            buf.append(")");
            node = node.prev;
        }
        buf.append("]");
        return buf.toString();
    }
}

public final class Snake extends PathNode {
    public Snake(int i, int j, PathNode prev) {
        super(i, j, prev);
    }

    @Override
    public Boolean isSnake() {
        return true;
    }
}

public final class DiffNode extends PathNode {
    public DiffNode(int i, int j, PathNode prev) {
        super(i, j, prev);
    }

    @Override
    public Boolean isSnake() {
        return false;
    }
}

• 寻找最优路径 及 解析diff

public class MyersDiff<T> {
    /**
     * 默认相等规则
     */
    private final Equalizer<T> DEFAULT_EQUALIZER = (original, revised) -> original.equals(revised);
    private final Equalizer<T> equalizer;

    public MyersDiff() {
        equalizer = DEFAULT_EQUALIZER;
    }

    public MyersDiff(Equalizer<T> equalizer) {
        this.equalizer = equalizer;
    }
    /**
     * 寻找最优路径
     */
    public PathNode buildPath(List<T> orig, List<T> rev) throws Exception {
        if (orig == null)
            throw new IllegalArgumentException("original sequence is null");
        if (rev == null)
            throw new IllegalArgumentException("revised sequence is null");
        final int N = orig.size();
        final int M = rev.size();
        //最大步数（先全减后全加）
        final int MAX = N + M + 1;
        final int size = 1 + 2 * MAX;
        final int middle = size / 2;
        //构建纵坐标数组（用于存储每一步的最优路径位置）
        final PathNode diagonal[] = new PathNode[size];
        //用于获取初试位置的辅助节点
        diagonal[middle + 1] = new Snake(0, -1, null);
        //外层循环步数
        for (int d = 0; d < MAX; d++) {
            //内层循环所处偏移量，以2为步长，因为从所在位置走一步，偏移量只会相差2
            for (int k = -d; k <= d; k += 2) {
                //找出对应偏移量所在的位置，以及它上一步的位置（高位与低位）
                final int kmiddle = middle + k;
                final int kplus = kmiddle + 1;
                final int kminus = kmiddle - 1;
                //若k为-d，则一定是从上往下走，即i相同
                //若diagonal[kminus].i < diagonal[kplus].i，则最优路径一定是从上往下走，即i相同
                int i;
                PathNode prev;
                if ((k == -d) || (k != d && diagonal[kminus].i < diagonal[kplus].i)) {
                    i = diagonal[kplus].i;
                    prev = diagonal[kplus];
                } else {
                    //若k为d，则一定是从左往右走，即i+1
                    //若diagonal[kminus].i = diagonal[kplus].i，则最优路径一定是从左往右走，即i+1
                    i = diagonal[kminus].i + 1;
                    prev = diagonal[kminus];
                }
                //根据i与k，计算出j
                int j = i - k;
                //上一步的低位数据不再存储在数组中（每个k只清空低位即可全部清空）
                diagonal[kminus] = null;
                //当前是diff节点
                PathNode node = new DiffNode(i, j, prev);
                //判断被比较的两个数组中，当前位置的数据是否相同，相同，则去到对角线位置
                while (i < N && j < M && equals(orig.get(i), rev.get(j))) {
                    i++;
                    j++;
                }
                //判断是否去到对角线位置，若是，则生成snack节点，前节点为diff节点
                if (i > node.i)
                    node = new Snake(i, j, node);
                //设置当前位置到数组中
                diagonal[kmiddle] = node;
                //达到目标位置，返回当前node
                if (i >= N && j >= M) {
                    return diagonal[kmiddle];
                }
            }
        }
        throw new Exception("could not find a diff path");
    }

    private boolean equals(T orig, T rev) {
        return equalizer.equals(orig, rev);
    }

    /**
     * 打印diff
     */
    public void buildDiff(PathNode path, List<T> orig, List<T> rev) {
        List<String> result = new ArrayList<>();
        if (path == null)
            throw new IllegalArgumentException("path is null");
        if (orig == null)
            throw new IllegalArgumentException("original sequence is null");
        if (rev == null)
            throw new IllegalArgumentException("revised sequence is null");
        while (path != null && path.prev != null && path.prev.j >= 0) {
            if (path.isSnake()) {
                int endi = path.i;
                int begini = path.prev.i;
                for (int i = endi - 1; i >= begini; i--) {
                    result.add("  " + orig.get(i));
                }
            } else {
                int i = path.i;
                int j = path.j;
                int prei = path.prev.i;
                if (prei < i) {
                    result.add("- " + orig.get(i - 1));
                } else {
                    result.add("+ " + rev.get(j - 1));
                }
            }
            path = path.prev;
        }
        Collections.reverse(result);
        for (String line : result) {
            System.out.println(line);
        }
    }
}

• 测试及结果

public static void main(String[] args) {
    String oldText = "A\nB\nC\nA\nB\nB\nA";
    String newText = "C\nB\nA\nB\nA\nC";
    List<String> oldList = Arrays.asList(oldText.split("\\n"));
    List<String> newList = Arrays.asList(newText.split("\\n"));
    MyersDiff<String> myersDiff = new MyersDiff<>();
    try {
        PathNode pathNode = myersDiff.buildPath(oldList, newList);
        System.out.println(pathNode);
        myersDiff.buildDiff(pathNode, oldList, newList);
    } catch (Exception e) {
        e.printStackTrace();
    }
}

[(7,6)(7,5)(6,4)(5,4)(3,2)(3,1)(2,0)(1,0)(0,0)(0,-1)]
- A
- B
  C
+ B
  A
  B
- B
  A
+ C

注意

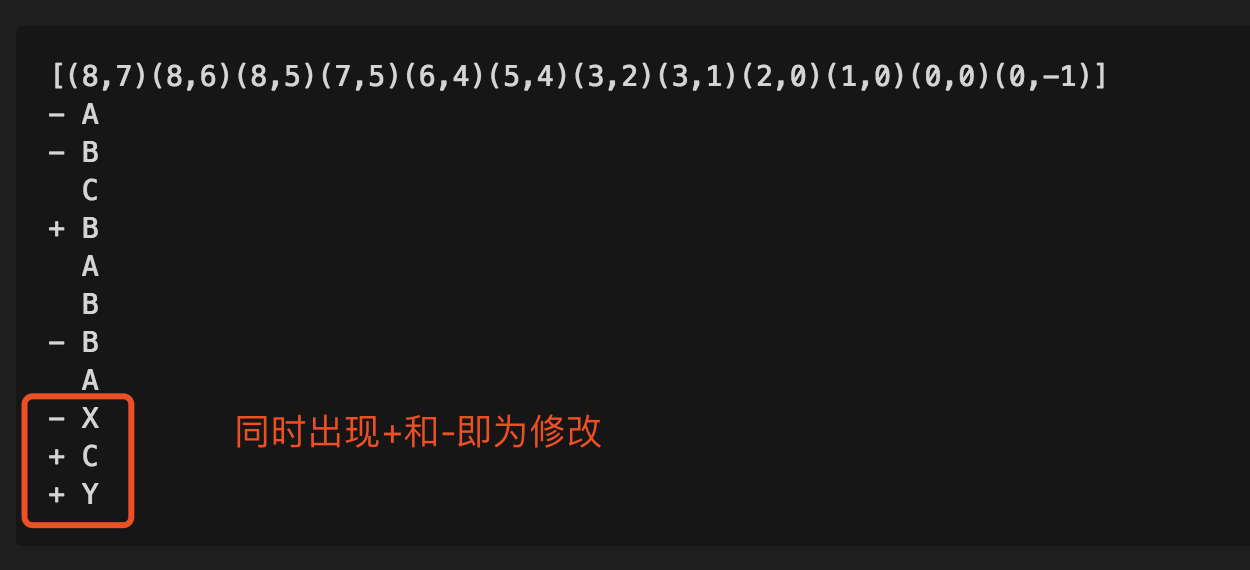
在git中不只是有增加和删除，还有修改，修改的原理是同时出现增加和删除，即为修改

时间复杂度

传统diff使用的是最naive的LSC计算算法（LCS:最长公共子序列），时间复杂度是O(M*N)（M,N分别为src与target的序列长度）

Myers的diff算法更好，时间复杂度为O((M+N)*D)（D为src与target的距离长度）尤其是在src与target相近时时间复杂度接近O(M+N)

延伸：动态规划

差分算法是典型的动态规划算法，动态规划算法是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决

动态规划算法的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解

例子一

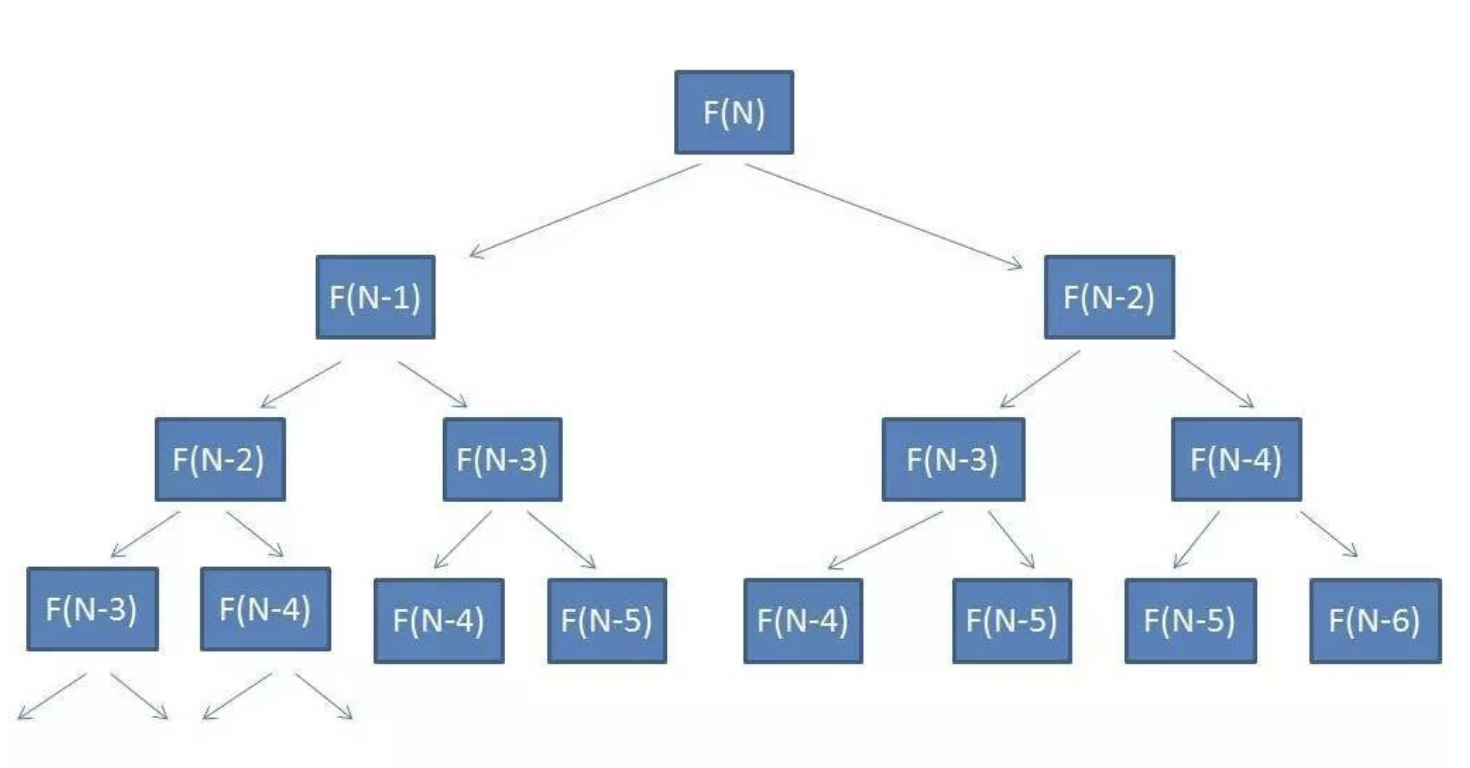
我们有个题目：有一座高度是10级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。

根据题目我们可以确定F(10)=F(8)+F(9)，即：从0到10级台阶的走法数量=从0到8级台阶的走法数量+从0到9级台阶的走法数量，则可推出如下公式：

F(1) = 1
F(2) = 2
F(n) = F(n-1)+F(n-2)（n>=3）

重要概念

• 最优子结构：F(8)和F(9)是F(10)的最优子结构

• 边界：F(1)和F(2)是问题的【边界】，如果一个问题没有边界将永远无法得到有限的结果

• 状态转移方程：F(n)=F(n-1)+F(n-2)是阶段与阶段之间的【状态转移方程】，这是动态规划的核心，决定了问题的每一个阶段和下一阶段的关系

实现逻辑

• 方法一：递归求解，时间复杂度：O(N^2）

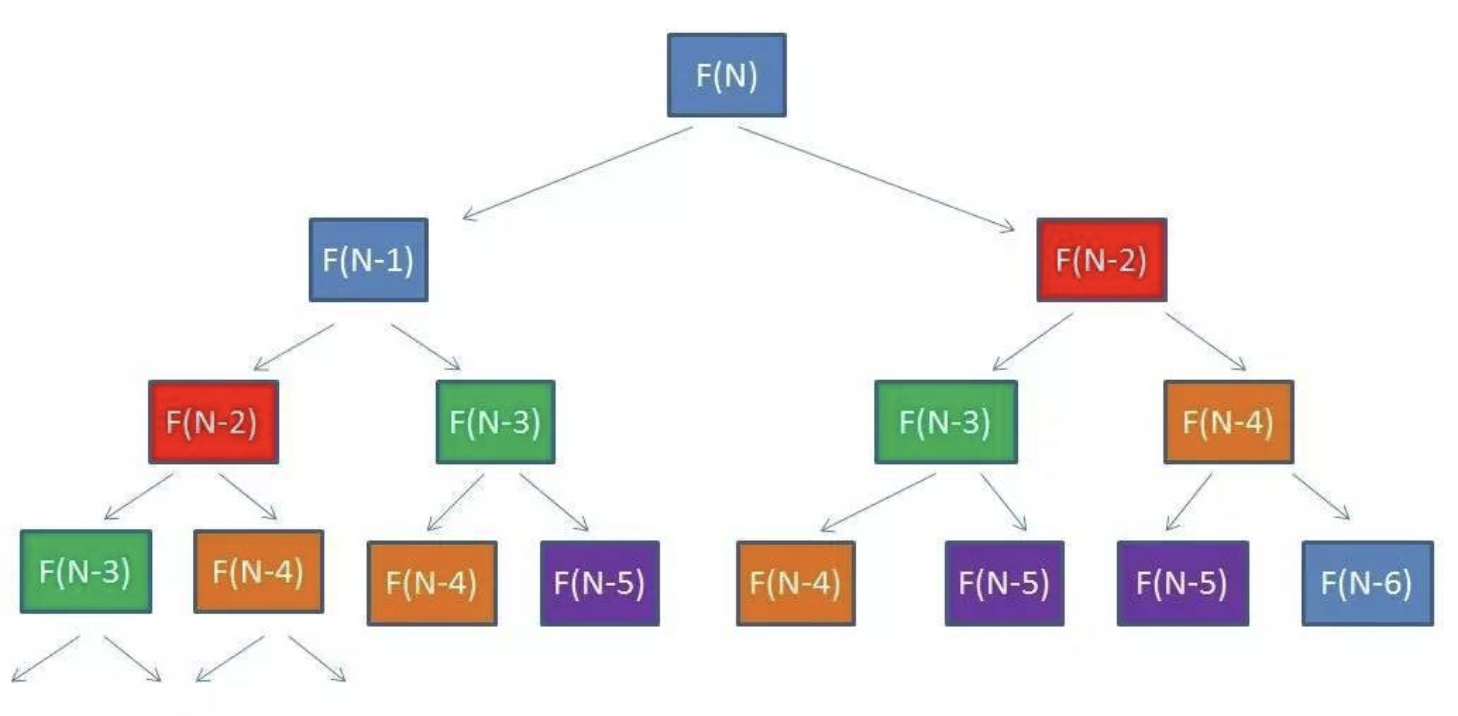
• 方法二：备忘录算法，缓存已经计算过的值，时间复杂度：O(N)，空间复杂度：O(N)

• 方法三：思路逆转，从底往上算，每次只需要存储前一次的值，时间复杂度：O(N)，空间复杂度：O(1)

参考文献

• Git是怎样生成diff的：Myers算法
• Myers论文
• Myers 差分算法 (Myers Difference Algorithm)
• Myers Diff Algorithm - Code & Interactive Visualization
• github-google开源工具：java-diff-utils
• demo