抽象思维
抽象思维是我们工程师最重要的思维能力。因为软件技术 本质上就是一门抽象的艺术。我们的工作是存思维的“游戏”,虽然我们在使用键盘、显示器,打开电脑可以看到主板、硬盘等硬件。但我们即看不到程序如何被执行,也看不到0101是如何被CPU处理的。
什么是抽象
简单而言,“抽”就是抽离,“象”就是具象,字面上理解抽象,抽象的过程就是从“具象”事物中归纳出共同特征,“抽取”得到一般化(Generalization)的概念的过程。英文的抽象——abstract来自拉丁文abstractio,它的原意是排除、抽出。
软件中的分层抽象无处不在
越是复杂的问题越需要分层抽象,分层是分而治之,抽象是问题域的合理划分和概念语义的表达。不同层次提供不同的抽象,下层对上层隐藏实现细节,通过这种层次结构,我们才有可能应对像网络通信、云计算等超级复杂的问题。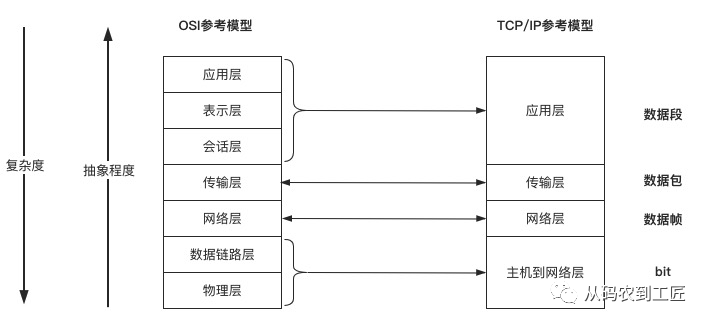
如何提升抽象思维能力
多阅读
为什么阅读书籍比看电视更好呢?因为图像比文字更加具象,阅读的过程可以锻炼我们的抽象能力、想象能力,而看画面的时候会将你的大脑铺满,较少需要抽象和想象。
这也是为什么我们不提倡让小孩子过多的暴露在电视或手机屏幕前的原因,因为这样不利于他抽象思维的锻炼。
抽象思维的差别让孩子们的学习成绩从初中开始分化,许多不能适应这种抽象层面训练的,就去读技校了,因为技校比大学会更加具象:车铣刨磨、零部件都能看得见摸得着。体力劳动要比脑力劳动来的简单。
多总结沉淀
小时候不理解,语文老师为什么总是要求我们总结段落大意、中心思想什么的。现在回想起来,这种思维训练在基础教育中是非常必要的,其实质就是帮助学生提升抽象思维能力。
记录也是很好的总结习惯。就拿读书笔记来说,最好不要原文摘录书中的内容,而是要用自己的话总结归纳书中的内容,这样不仅可以加深理解,而且还可以提升自己的抽象思维能力。
我从四年前开始系统的记录笔记,做总结沉淀,构建自己的知识体系。这种思维训练的好处显而易见,可以说我之前写的《从码农到工匠》和现在正在写的《程序员必备的思维能力》都离不开我总结沉淀的习惯。
命名训练
每一次的变量命名、方法命名、类命名都是一次难得的抽象思维训练机会,前面已经说过了,语言和抽象是一体的,命名的好坏直接反应了我们的问题域思考的是否清晰,反应了我们抽象的是否合理。
现实情况是,我们很多的工程师常常忽略了命名的重要性,只要能实现业务功能,名字从来就不是重点。
实际上,这是对系统的不负责任,也是对自己的不负责任,更是对后期维护系统的人不负责任。写程序和写文章有很大的相似性,本质上都是在用语言阐述一件事情。试想下,如果文章中用的都是些词不达意的句子,这样的文章谁能看得懂,谁又愿意去看呢。
同样,我一直强调代码要显性化的表达业务语义,其中命名在这个过程中扮演了极其重要的角色。为了代码的可读性,为了系统的长期可维护性,为了我们自身抽象思维的训练,我们都不应该放过任何一个带有歧义、表达模糊、意不清的命名。
领域建模训练
对于技术同学,我们还有一个非常好的提升抽象能力的手段——领域建模。当我们对问题域进行分析、整理和抽象的时候,当我们对领域进行划分和建模的时候,实际上也是在锻炼我们的抽象能力。
我们可以对自己工作中的问题域进行建模,当然也可以通过阅读一些优秀源码背后的模型设计来学习如何抽象、如何建模。比如,我们知道Spring的核心功能是Bean容器,那么在看Spring源码的时候,我们可以着重去看它是如何进行Bean管理的?它使用的核心抽象是什么?不难发现,Spring是使用了BeanDefinition、BeanFactory、BeanDefinitionRegistry、BeanDefinitionReader等核心抽象实现了Bean的定义、获取和创建。抓住了这些核心抽象,我们就抓住了Spring设计主脉。
除此之外,我们还可以进一步深入思考,它为什么要这么抽象?这样抽象的好处是什么?以及它是如何支持XML和Annotation(注解)这两种关于Bean的定义的。
这样的抽象思维锻炼和思考,对提升我们的抽象能力和建模能力非常重要。关于这一点,我深有感触,初入职场的时候,当我尝试对问题域进行抽象和建模的时候,会觉得无从下手,建出来的模型也感觉很别扭。然而,经过长期的、刻意的学习和锻炼之后,很明显可以感觉到我的建模能力和抽象能力都有很大的提升。不但分析问题的速度更快了,而且建出来的模型也更加优雅了
小结
- 抽象思维是程序员最重要的思维能力,抽象的过程就是寻找共性、归纳总结、综合分析,提炼出相关概念的过程。
- 语言和抽象是一体的,抽象思维也叫词思维,因为抽象的概念只能通过语言才能表达出来。
- 抽象是有层次性的,抽象层次越高,内涵越小,外延越大,扩展性越好;反之,抽象层次越低,内涵越大,外延越小,扩展性越差,但语义表达能力越强。
- 对抽象层次的拿捏,体现了我们的设计功力,视具体情况而定,抽象层次既不能太高,也不能太低。
- 重复代码意味着抽象缺失,强制类型转换意味着抽象层次有问题,我们可以利用这些信号来重构代码,让代码重新变得优雅。
- 我们可以通过刻意练习来提升抽象能力,这些练习包括阅读、总结、命名训练、建模训练等。
结构化思维
结构化思维是一种从无序到有序、从混乱到清晰的思维能力,可以帮助我们快速加工处理繁杂的信息,提炼要点,从而更加清晰的表达。
什么是结构
结构可以说是万物之本。大到宇宙星系,小到尘埃颗粒,任何事物都有其特定的结构,这些事物也是通过其特定的结构来体现其存在的价值和意义。
在系统论中,系统是处在一定环境下各组成部分的整体,我们把这各个组成部分,称之为系统的要素。很显然,系统不只是要素的简单加和,而是有什么内在的东西实现了各要素的普遍联系。我们就把这种各要素的组织形式(要素之间的关系)称之为结构。
系统的性质是由结构决定的。要素的内容是不稳定的,可能随时会被替换。就像忒休斯之船,虽然船的木板被换掉了,但只要船的结构没有变,其仍然是忒休斯之船;中国的两千年封建历史也是一样,皇帝(要素)一个接一个的换,但是本质上,其背后的皇权剥削制度没有变,旧社会的结构没有变,所以皇帝的更替,并没有改变封建社会的本质。
我们通常说的“结构性问题”,就是指那些底层的、难以改变的根本性问题。经济上的结构性问题就是作为经济这个系统的结构的经济制度,分配制度和所有制等等出现了问题。
在冰山之下,深层次还是结构问题
什么是结构化思维
结构如此重要,它反映了系统要素的组织形式,决定了系统性质。那有没有一种方法来帮助我们发现结构,或者帮助我们搭建结构呢?
有的,这就是我们接下来要介绍的结构化思维。所谓的结构化思维,就是从无序到有序的一种思考过程,将搜集到的信息、数据、知识等素材按一定的逻辑进行分析、整理,呈现出有序的结构,继而化繁为简。有结构的信息更适合大脑记忆和理解。
为什么是金字塔结构
说到结构化思维,就不得不提到结构化思维的圣经——芭芭拉·明托的《金字塔原理》。这本书我反复读过多遍,在业界也有很好的口碑,美团王兴说:“仔细认真读完这本书,是员工在美团能否成功的基本功。它是美团四大名著之首,也是美团能力跃迁,职级晋升的官方推荐必读书籍,它就是《金字塔原理》” 上文已经说过,结构化思维很有用,但为什么是金字塔结构呢?这和我们大脑的思维过程有关,人类很早以前就认识到,大脑会自动将发现的所有事物以某种秩序组织起来。基本上,大脑会认为同时发生的任何事物之间都存在某种联系,并且会将这些事物某种逻辑模式组织起来。
“有逻辑”和“没有逻辑”对我们大脑的理解和记忆起着至关重要的作用。
当你在听别人讲话、看文章、阅读代码的时候,也会发生类似的组织思想的现象。你会将同时出现的或位置相邻的几个思想相联系,努力用某种逻辑模式组织他们。这种逻辑模式必定是金字塔结构的,因为只有金字塔结构才能够满足大脑的两个需求:
- 概念不能多:大脑一次记忆很难超过7个思想、概念或项目。
- 有逻辑关系:大脑容易记住有逻辑关系的事物。
也就是说,如果我们能按照金字塔的结构准备我们的演讲、写文章、写代码,因为其满足我们大脑处理信息的特点——概念不能多,有逻辑关系,我们的听众和读者会更容易理解我们要表达的思想。对应到我们工程领域,即满足金字塔原理的代码,其可读性和可理解性会极大的被增强,代码也是一种表达,很多人以为代码是写给机器执行的,实际上,代码是写给人读的,只是偶尔会被机器执行。
我们平时说的构建自己的知识体系,实际上就是在构建这个巨大的金字塔结构。
金字塔结构里的逻辑
逻辑是指对象之间的关系,这个关系可以是演绎关系、因果关系、空间关系、程度关系、并列关系、类比关系等等。所谓的“有逻辑”,就是这个“关系”是合乎理性的,道理是通顺的。逻辑是我们认知的基础,在结构中起着至关重要的作用。好的结构,离不开清晰、有效的逻辑,只有理清逻辑关系,才能正真的化繁为简,否则即使你搭建了结构,依然逃不脱那一片混沌。
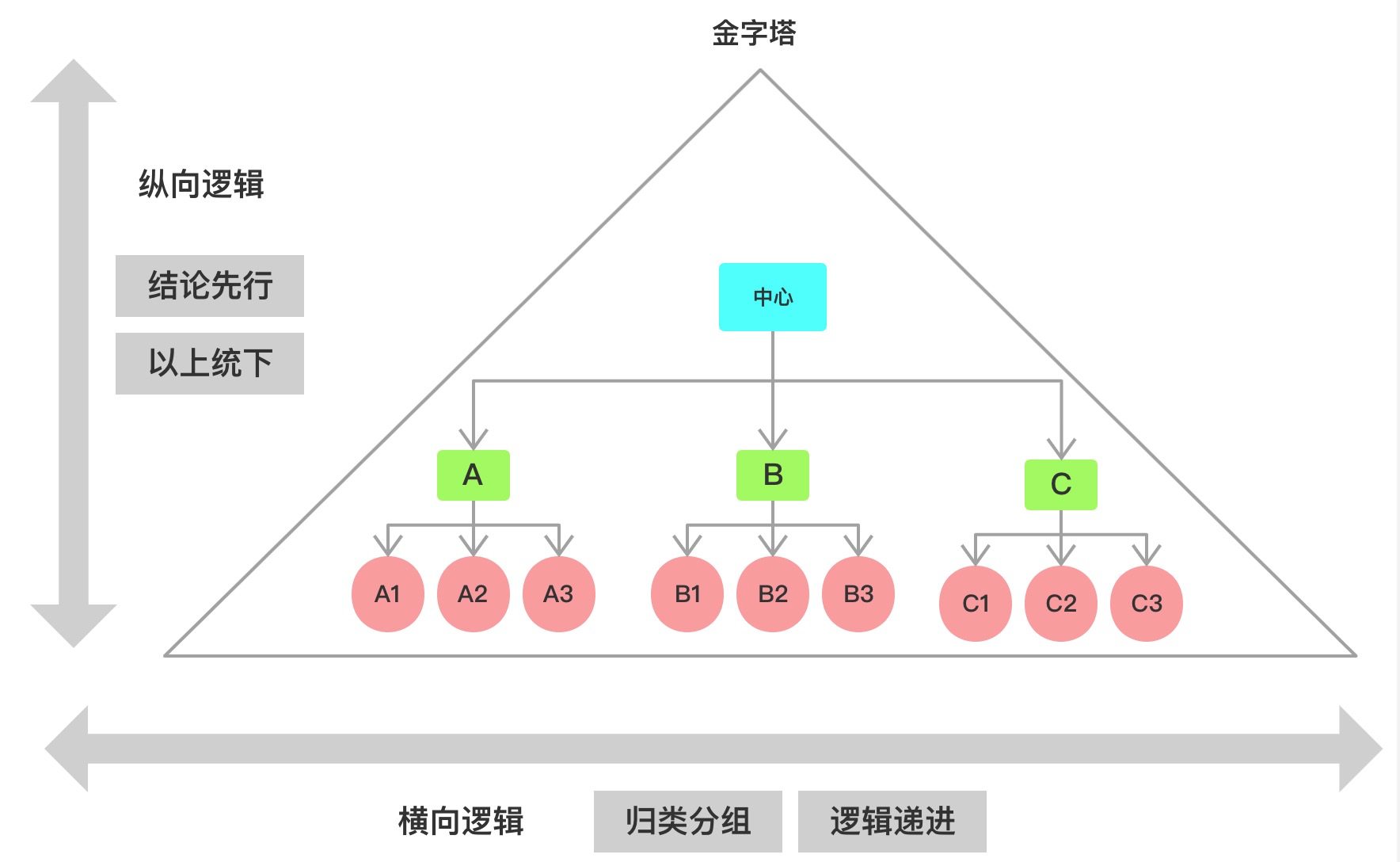
在金字塔结构中,总体上有两个方向的逻辑关系,即纵向逻辑关系和横向逻辑关系。一个好的金字塔结构,需要在纵向关系上满足结论先行、以上统下;在横向关系上,满足归类分组、逻辑递进这四个基本原则。用一句话概括,就是“论证类比”。
金字塔结构:纵向逻辑关系
金字塔的纵向上,体现的主要是金字塔的层次关系。在构建这个层次关系的过程中,我们需要动用我们在组织思想时,仅有的两个逻辑推理能力:演绎逻辑和归纳逻辑。也就是我们所谓的形式逻辑。
演绎逻辑
演绎逻辑是一个从一般到特殊的过程。我们通常说的“大前提、小前提、结论”的三段论形式就是典型的演绎逻辑。

归纳逻辑
归纳逻辑比演绎逻辑要难,因为归纳需要我们有很好的抽象能力,抽象出新的概念,去统领其下面的子概念。
金字塔结构:横向逻辑关系
横向上,我们要保证每组思想必须属于同一逻辑范畴,并按照逻辑顺序进行组织。即你组织在一起的思想不是随意堆放在一起,而是你看到了其中的逻辑关系,才将其“挑选”出来组织在一起。实际上,大脑在进行归纳分组的逻辑分析时,只有以下3种分析活动:
- 时间顺序:例如解决问题的3个步骤。
- 空间顺序:例如组成某公司的3个部门,化整为零(将整体分解为部分)等都是空间顺序。
- 程度顺序:某公司存在的最严重的3个问题。
时间顺序
时间顺序,是最容易理解的逻辑顺序,也是使用最广泛的思想分组。在要按照采取行动的顺序(第一步、第二步、第三步….)依次表达达到某一结果必须采取的行动。
空间顺序
空间顺序,是一种化整为零的分解,比如对公司组成部门和地理位置的分解。再将整某个整体(不论是客观存在的还是概念性的整体)划分为不同的部分时,你必须保证划分后的各部分符合以下要求:
- 各部分之间相互独立(mutually exclusive):没有重叠,有排他性。
- 所有部分完全穷尽(collectively exhaustive):没有遗漏。
这两个要求简称是MECE原则
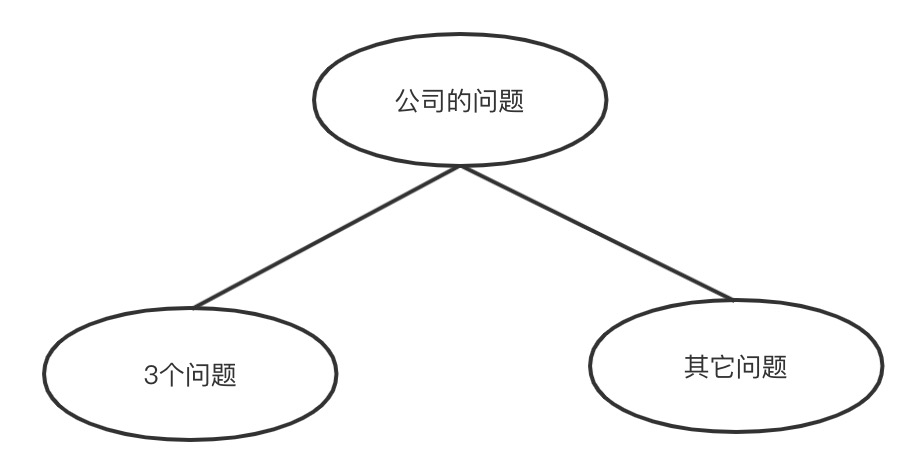
程度顺序(重要性顺序)
程度顺序,也称为重要性顺序。是你对一组因为具有某种共同特点而被聚集在一起的事务所采用的顺序。如:3个问题,3个原因,3个因素等。在为事物分组时,你可能会说:“这家公司存在3个问题。” 这时,你的大脑自动将这个3个问题和其它问题 隔开。也就是说,这个3个问题是你认为这个公司最严重、最迫切需要解决的问题,于此同时,公司可能还存在很多其它的问题,你只挑选这3个,是因为这3个最重要。在排序的时候,最好是先重要后次要(first thing first),先强后弱。
如何构建结构
我们在解决问题的时候,一般有两种方法:一种是从目标出发沿着不同的路径分解,探求问题的答案;另一种是把各种信息聚合起来,得出一个正确结论或解决方案。这两种方法也是我们构建金字塔结构时仅有的两种方法:一是自上而下的搭建金字塔结构,即问题分解,也叫疑问回答分解;二是自下而上搭建金字塔结构,即概括总结做聚合。
- 自上而下
当我们明确知道要解决的问题是什么的时候,可以考虑自下而上的方式,对问题进行拆解。比如你要去准备竞聘,这是一个非常的明确的目标,就比较合适做自上而下的分解。
- 自下而上
有些时候,我们要解决的问题并没有那么明确,或者面对的是一堆零散的元素,比如我们在头脑风暴的时候,产出了很多想法,我们要如何整理这些想法,此时,我们要如何构建清晰的结构呢?我们可以用结构化思维,对同类信息,进行归纳分组,向上聚合形成一个金字塔的结构。分组的逻辑是要找到共性,并归为一类。
2W1H法
2W1H是构建结构最常用,也是最有用的框架之一,因为它涉及到一个问题的最核心的3个要素。
有了2W1H这个思考框架,我对“如何写好技术文章”进行了自上而下的结构搭建,接下来,写出这篇元技能文章,也就不是什么难事了:
- 为什么写文章:1)写文章是费曼学习法。2)写文章可以增加影响力。
- 什么是好文章:1)内容有价值。2)结构要清晰。
- 如何写好文章:1)选择好内容。2)搭建清晰的结构。3)刻意练习。4)迭代优化。
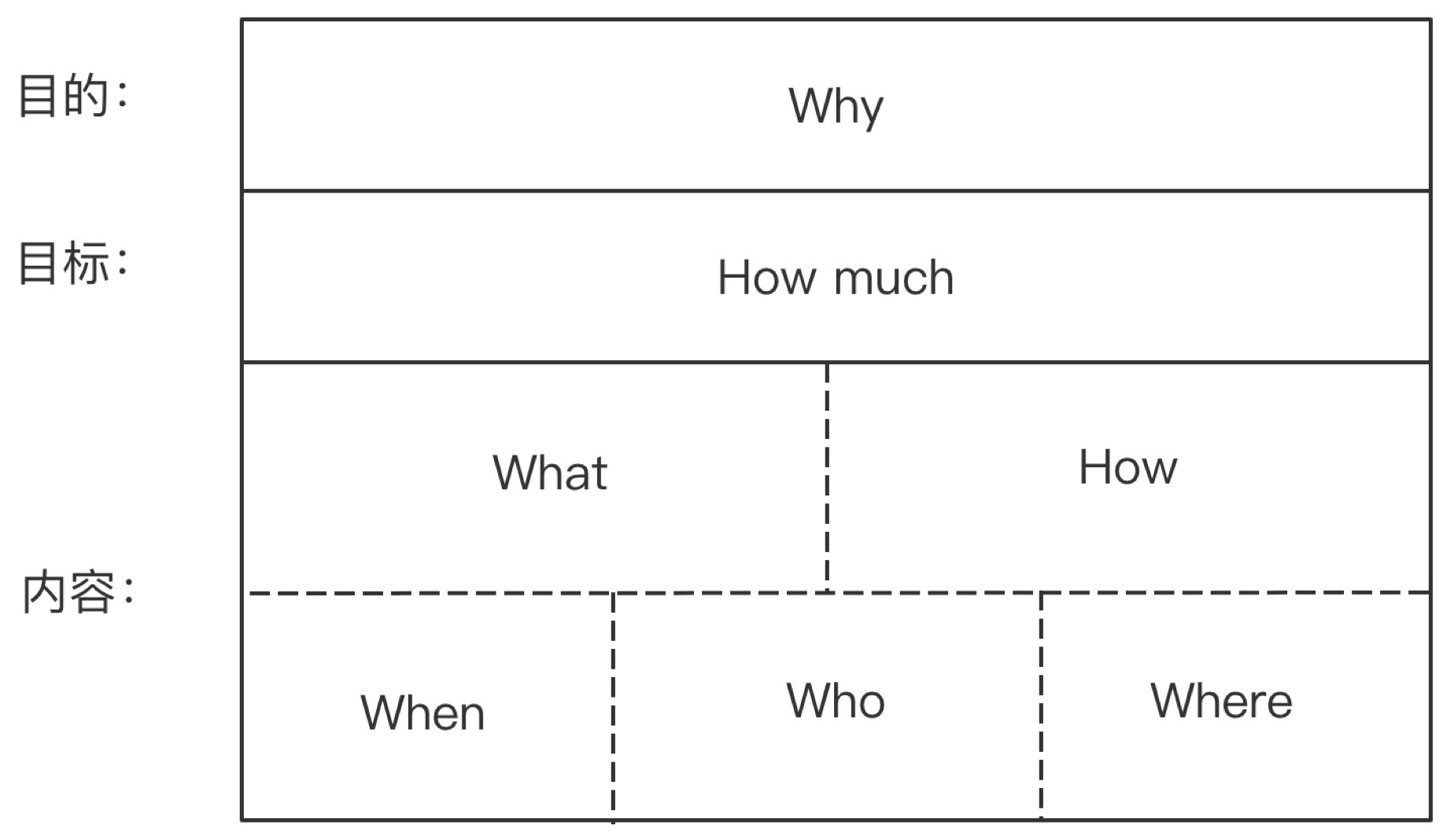
2W1H实际上是对5W2H(Why、Who、When、Where、What、How和How much)的简化和提炼,如果需要更加全面的思考,我们需要尽量满足MECE法则,此时,5W2H可能是更好的选择。
5Why分析法
另外,我们还可以用“疑问解答”的方式来自上而下的构建我们的结构,这样做的好处是,一方面可以通过设置悬念抓住听者的注意力,另一方面这种不断问“为什么?”的方式,也是在帮助我们更加深入的理解问题,让我们的论证更加有说服力。
实际上,对于大部分的问题,如果你能连续追问5个why(为什么),一般都能触及问题的本质,所以这种通过疑问——解答的方式自上而下的构建结构,不仅是一种构建结构的方法,也是一种发现问题根源的强大武器——5why分析法。
例如,丰田汽车公司前副社长大野耐一曾举了一个通过5why分析法来找出停机的真正原因。
问题一:为什么机器停了? 答案一:因为机器超载,保险丝烧断了。
问题二:为什么机器会超载? 答案二:因为轴承的润滑不足。
问题三:为什么轴承会润滑不足? 答案三:因为润滑帮浦失灵了。
问题四:为什么润滑帮浦会失灵? 答案四:因为它的轮轴耗损了。
问题五:为什么润滑帮浦的轮轴会耗损? 答案五:因为杂质跑到里面去了。
经过连续五次不停地问“为什么”,才找到问题的真正原因和解决的方法,在润滑帮浦上加装滤网。 如果员工没有以这种追根究底的精神来发掘问题,他们很可能只是换根保险丝草草了事,真正的问题还是没有解决。
5W2H法
通过前面的介绍,我相信你在学习结构化思维的同时,应该也感受到了思维框架在结构化中的作用,比如2W1H就是非常有用的框架,因为它涉及到大部分问题的本质——“是什么”,“为什么”,“如何做”。
5W2H也是解决一般问题非常有用的思维框架,5W2H分别代表Why、Who、When、Where、What、How和How much,很多问题都可以拆解成这7个要素,如果你知晓这个结构,在分析问题的时候,就比不知道这个结构的人要更加全面和体系化。知晓框架的好处是,别人的难题,只是你的“填空题”,别人在感叹你思考为什么如此全面的时候,你会心一笑,这只不过是一个“套路”。
逻辑思维
在日常交流中,我们会频繁的使用“逻辑”这个词。但能够清晰的说出逻辑的定义(什么是逻辑)应该不多,能够正确的掌握逻辑推理的人就应该更少了。
什么是逻辑
逻辑是指思维的规律和规则。逻辑除了指思维规律,狭义上,也有逻辑学的含义,按照《逻辑学导论》中的定义,逻辑学是研究用于区分正确推理(inference)与不正确推理的方法和原理的学问。
相比较上面的教科书定义,我觉得芝本秀德在《深度思考法》中对逻辑的定义要更容易理解,他说“逻辑就是关系。”
我们说某人逻辑性太差,其实正是因为他们没有在想表达东西之间建立关系。例如,对方说“今天的天气真不错。”我们认为,诸如“是啊,天气太好了”或者“天气让人心情都变好了”这样的回答是有逻辑性的。可是如果回答是“我肚子好饿啊”,那么这种答非所问,就完全不符合逻辑。所以说无逻辑就是没有建立起事物之间的正确关系,换句话说有逻辑就是能建立事物之间的正确关系。
逻辑思维的要素
逻辑思维基本包含三个方面:
- 概念;
- 判断(在逻辑学中,也叫命题,英文是proposition);
- 推理(在逻辑学中,也叫论证,英文是argument);
概念是思维的基本单位;通过概念对事物是否具有某种属性进行肯定或否定的回答,这就是判断;由一个或几个判断推出另一判断的思维形式,就是推理。
所以逻辑思维的要义,就在于正确运用概念、判断、推理的思维形式。想要正确掌握逻辑思维,就必须从这三方面学起。
概念
概念是思维的基本单位,是反映事物本质属性或特有属性的思维形式。
这个世界有很多事物,都是通过我们的思维去赋予它们意思或意义的,然后通过语言符号呈现出来。所以说,这些意思或意义,就是概念的思维内显形式。语言是概念的外显形式。
判断
判断(也叫命题)是推理的建筑基块,一个判断就是一个断言(Assert),它断定了一个事情是这样或者不是这样。因此,每一个判断都是或真或假的。
判断是概念的展开,没有判断,就不能揭示和说明概念。同时,判断也是推理的前提,是正确运用各种推理的必要条件。准确的运用判断,我们才能够进行正确的思考。而思考的形式,就是推理了。
逻辑推理
逻辑推理,可以分为演绎推理(Deductive Inference)、归纳推理(Inductive Inference)和溯因推理(Abductive Inference)。 还记得上文关于逻辑的定义吗,逻辑就是关系。所谓的推理,就是研究语句、判断、命题之间相互关系的学问。
演绎推理
演绎推理旨在阐明前提和结论之间的关系,为评估演绎论证是否有效提供方法。
演绎逻辑是一个从一般到特殊的过程。我们通常说的“大前提、小前提、结论”的三段论形式就是典型的演绎逻辑。例如“所有人都会死,苏格拉底是一个人,因此,苏格拉底会死。” 大前提是“所有人都会死”,小前提是“苏格拉底是一个人”,结论是“苏格拉底会死。” 这是一种必然性推理(保真推理),因为其结论就包含在前提之中,“所有人会死”本身就包含“苏格拉底会死”。
演绎逻辑,在历史上出现了两种杰出理论。第一种被称为“古典逻辑”或“亚里士多德逻辑”,开创这种理论的是古希腊哲学家亚里士多德,他关于推理的论述被收集成册,称为《工具论》。另一种称为“现代逻辑”或“现代符号逻辑”,他主要形成与20世纪。
归纳推理
归纳推理是以一类事物中若干个别对象的具体知识为前提,推出有关该类事物的普遍性知识的结论的过程。
例如:
猫A喜欢吃鱼。
猫B喜欢吃鱼。
猫C喜欢吃鱼。
猫D喜欢吃鱼。
因此:猫喜欢吃鱼。
溯因推理
溯因推理就是我先知道了答案,再去追溯原因的推理。这种推理方法最早也是由亚里斯多德提出的,在他的著作《前分析篇》中,提到过一种“还原推理模式”,说的正是溯因推理。
演绎推理的方法是由A推理出B,而溯因推理则不同,它是在看到了B后,推理出到底是什么导致了B的最佳解释方法,可以理解成是根据结果B去推测原因A的推理方法。换句话说,溯因推理是解释已知事物的过程。
如何进行溯因推理呢?简单来说,就是八个字:大胆假设,小心求证。
逻辑谬误
所谓谬误(fallacy),就是推理中的欺骗手段,常见的花招有错误假设,理由和结论不相关(偷换概念)等。谬误包括偷换概念、错误假设、以偏概全、转移话题、人身攻击、以势压人、以众压人、循环论证、不适当地诉诸权威、不适当地诉诸情感、窃取论题、 得寸进尺等等。
偷换概念
偷换概念也是一种常见的诡辩手法。主要有以下几种表现:
- 任意改变一个概念的内涵和外延.使之变成另一个概念。
- 利用多义词可以表达几个不同概念的特点,故意把不同的概念混淆起来。
- 抓住概念之间的某些相似之处,抹杀不同概念的本质区别。
错误假设
在所有的论证中,都有一些作者认为是理所当然的特定假设,通常情况下他们却不会明说出来。因此,乍一看,几乎每个论证都显得“有道理”,其外表结构看起来都显得完美无缺。但有些内在的没有说出来的看法——隐含假设,所起到的作用同样重要。
循环论证
一个结论会自己证明自己,只不过措辞有所改变。
例如:
老马:“可是什么有意义呢,许三多?人这辈子绝大多数时候都在做没意义的事情。”
许三多:“有意义就是好好活。”
老马:“那什么是好好活呢?”
许三多:“好好活就是做有意义的事情。(看一眼老马后再强调)做很多很多有意义的事情。”
以偏概全
偏概全是指依据不充分的例证得出普遍的结论。你不能说看到3个意大利人很有情调,就说所有的意大利人都是浪漫的。以偏概全是使用归纳法中常见的谬误,即使用过小的样本量,或者不具代表性的样本,归纳得到一个错误的结论。
滑坡谬误
滑坡谬误是指不合理使用连串因果关系。通过一个起因A,引发多米诺效应,带来一些列负面事情。A并不是很糟糕,但是A导致B,B导致C,C导致D,D简直糟糕透顶。
例如:
现在的教育内卷,实际上也是一种滑坡谬误,很多家长不想让小孩输在起跑线上,认为没有好的幼儿园就上不了好小学,没有好小学就上不了好中学,没有好中学就上不了好大学,上不了好大学这辈子就没有希望了。
对于个人的落地事项
- 写好周报,表达内容要清晰明确
- 做好阅读计划、总结计划